卷积核心知识回顾
发现笔试选择题可能会考卷积的,在这里回顾一下卷积常考的一些知识点。
卷积计算公式
输入图片的尺寸假设为\(n\times n\),卷积核大小为\(f\times f\),padding大小为\(p\),步长为\(s\)时,输出特征图的尺寸\(o\times o\)可以用如下公式计算: \[ o = \lfloor \frac{n-f+2p}{s} \rfloor + 1 \]
多通道卷积
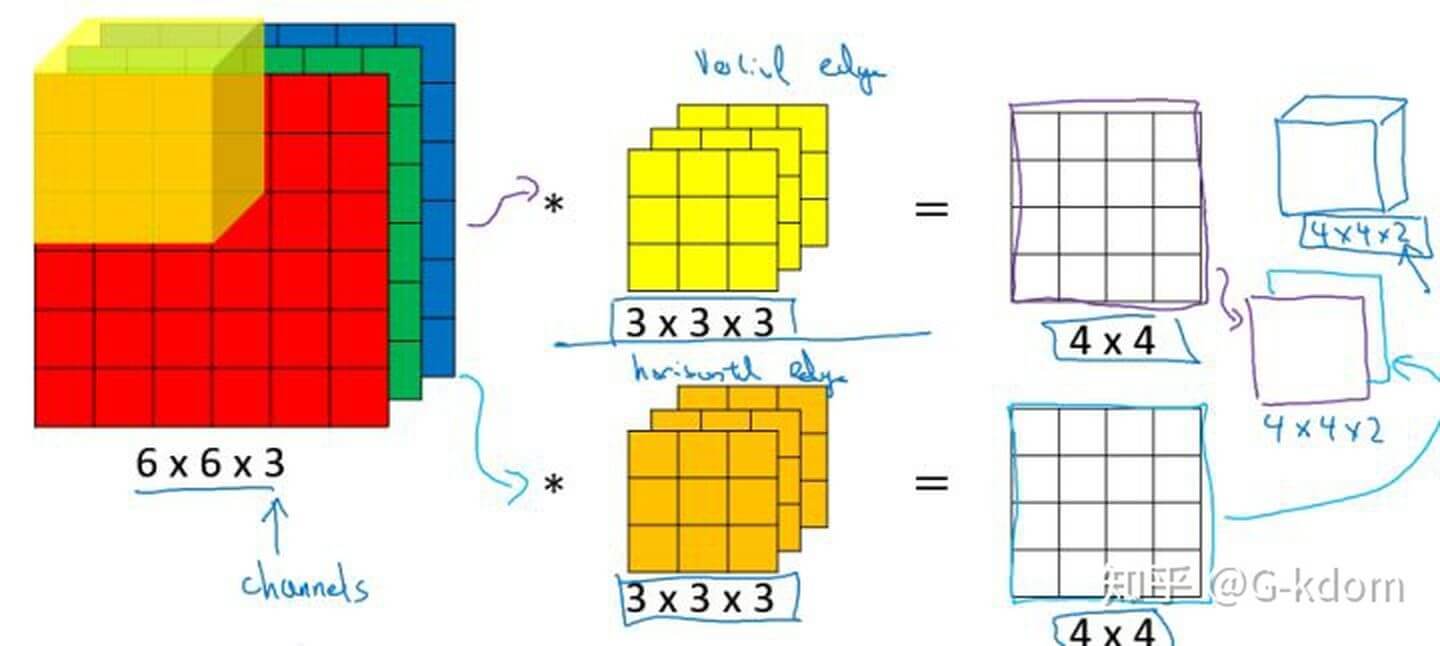
多通道卷积的计算过程:将矩阵与滤波器对应的每一个通道进行卷积运算,最后相加,形成一个单通道输出,加上偏置项后,我们得到了一个最终的单通道输出。如果存在多个filter,这时我们可以把这些最终的单通道输出组合成一个总输出。
这里我们还需要注意一些问题——滤波器的通道数、输出特征图的通道数。
某一层滤波器的通道数 = 上一层特征图的通道数。如上图所示,我们输入一张 6×6×3 的RGB图片,那么滤波器( 3×3×3 )也要有三个通道。
某一层输出特征图的通道数 = 当前层滤波器的个数。如上图所示,当只有一个filter时,输出特征图( 4×4 )的通道数为1;当有2个filter时,输出特征图(4×4×2 )的通道数为2。
FCN
一些CNN网络用卷积层替换了最后的全连接层,称之为全卷积神经网络FCN。
可行性方面:尽管卷积提取局部信息,但如果是“最大的局部”实际上等效于全局。
替代的好处:
- 用卷积层替换全连接层可以让卷积网络在一张更大的输入图片上滑动,得到每个区域的输出,这样就突破了此前对于图像输入尺寸的限制。
- 使特征图带有位置信息,从而可以实现基于像素的预测。
参考视频:https://www.youtube.com/watch?v=0nIMcnO_3b8
ResNet前几层的维度
输入是224x224的尺寸,经过kernel size为7,步长为2,padding为3的conv1,按照公式output=(Input-kernel+2padding)/stride+1 则有(224-7+23)/2+1=112.5≈112,此时输出尺寸为112; 再输入到layer1中,经过kernel size为3,步长为2,padding为1的maxpool 有(112-3+2)/2+1≈56,此时输出尺寸为56; 再输入到layer2中,经过kernel size为3,步长为2,padding为1的卷积 有(56-3+2)/2+1≈28,此时输出尺寸为28; 再输入到layer3中,经过kernel size为3,步长为2,padding为1的卷积 有(28-3+2)/2+1≈14,此时输出尺寸为14; 再输入到layer4中,经过kernel size为3,步长为2,padding为1的卷积 有(14-3+2)/2+1≈7,此时输出尺寸为7。