引言

起因是在leetcode上看到了这题：36. 有效的数独，这题其实是判断数独的初始盘面是不是有效的，即初始数字是否满足行、列和小方块里都不重复的条件。可以通过一次遍历解决。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution:
    def isValidSudoku(self, board: List[List[str]]) -> bool:
        # 一次遍历
        n = len(board)
        row_counter_list = [set() for _ in range(n)]
        col_counter_list = [set() for _ in range(n)]
        square_counter_list = [set() for _ in range(n)]

        for i in range(n):
            for j in range(n):
                num = board[i][j]
                if num == ".":
                    continue
                # 先行后列再方框
                if num in row_counter_list[i]:
                    return False
                else:
                    row_counter_list[i].add(num)

                if num in col_counter_list[j]:
                    return False
                else:
                    col_counter_list[j].add(num)
                
                row_index = i // 3
                col_index = j // 3
                square_index = row_index * 3 + col_index
                if num in square_counter_list[square_index]:
                    return False
                else:
                    square_counter_list[square_index].add(num)

        return True

因为数独的元素天生是数字，所以这里的counter实际上可以用数组表示。但为了方便使用in的语法，这里直接申请了集合，占用空间会大一些。

一开始看这道题的时候把我吓了一下，因为是做“有效的数独”，还以为要判断这个数独可不可解，解唯一不唯一才能判断“有效性”。看题面后发现是看初始条件有效就行了。那也引发一个问题，如果真的要解数独，或者要判断这个数独题目可不可解有办法做吗？

回溯法及框架

学过的算法加解题的技巧就下面几种： 1. 分治法（Divide-and-conquer method, DC） 2. 二分查找（Binary seach） 3. 双指针（Double point） 4. 滑动窗口（Sliding Window） 5. 贪心法（Greedy algorithm） 6. 动态规划（Dynamic promgraming, DP） 7. 回溯法（Backtracking）

因为不是查找问题，所以2，3，4可能都用不了。贪心法和动态规划一般用于求解最优化的问题，这里似乎也不太好用。分治法因为数独行、列和小方框之间都有联系，似乎不太好分治。因此选择回溯法去做，通过深度优先搜索和回溯来查找数独题面的可行解。

引用一下wiki上的解释：

回溯法（英语：backtracking）是暴力搜索法中的一种。

对于某些计算问题而言，回溯法是一种可以找出所有（或一部分）解的一般性算法，尤其适用于约束满足问题（在解决约束满足问题时，我们逐步构造更多的候选解，并且在确定某一部分候选解不可能补全成正确解之后放弃继续搜索这个部分候选解本身及其可以拓展出的子候选解，转而测试其他的部分候选解）。

在经典的教科书中，八皇后问题展示了回溯法的用例。（八皇后问题是在标准国际象棋棋盘中寻找八个皇后的所有分布，使得没有一个皇后能攻击到另外一个。）

回溯法采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程中，当它通过尝试发现，现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现，在反复重复上述的步骤后可能出现两种情况： - 找到一个可能存在的正确的答案 - 在尝试了所有可能的分步方法后宣告该问题没有答案

在最坏的情况下，回溯法会导致一次复杂度为指数时间的计算。

上算法课的时候老师总结了一个好用的回溯法思考框架：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
'''
The following is the algorithm framework and should not be modified.
'''
def dfs(v):
    advance(v)
    if isLeaf(v):
        remark(v)
    else:
        e = nextAdj(v, None)
        while e is not None:
            if not exceedBound(v + [e]):
                v.append(e)
                dfs(v)
            e = nextAdj(v, e)
    backtrack(v)

dfs([])

其辅助函数的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def nextAdj(v, e):
    '''
    The following 2 lines should not be modified.
    '''
    if e is None:
        e = 0  # Permutation Problem start by 1, while Subset Problem start by 0, e is its leader
    # Add the rest of the implementation for nextAdj if needed

def backtrack(v):
    if len(v) == 0:
        print('the end...')
    else:
        # print('backtracking from ' + str(v))
        del v[-1]

def isLeaf(v):
    if len(v) == n:
        return True
    else:
        return False

简单解释一下各个部分的含义：

  1. 函数 dfs(v)：
    • dfs 是深度优先搜索（Depth First Search）的缩写。v 是当前的部分解，即一个从起始状态到当前状态的路径或部分解集。
  2. 函数调用 advance(v)：
    • 这是一个占位符函数，通常用于在进入下一个递归调用前做一些初始化或准备工作。在具体实现中，可能包括更新状态、打印调试信息等。
  3. 条件检查 isLeaf(v)：
    • 检查当前部分解 v 是否已经达到叶子节点。叶子节点通常表示一种完全解或一种可接受的终止状态。
    • isLeaf(v) 函数定义了叶子节点的判定标准。例如，在排列问题中，当 v 的长度等于待排列元素的数量时，v 就是一个叶子节点。
  4. 函数调用 remark(v)：
    • 这是另一个占位符函数，通常用于处理或记录找到的完整解。例如，打印解、存储解或其他处理操作。
  5. 获取下一个邻接节点 e = nextAdj(v, None)：
    • nextAdj(v, None) 函数用于获取当前部分解 v 的第一个邻接节点。对于第一个调用，e 通常被初始化为 None。
    • 在具体问题中，邻接节点表示可以扩展当前部分解的下一个可能选择。
  6. 边界检查 if not exceedBound(v + [e])：
    • 检查扩展后的部分解 v + [e] 是否超过了问题定义的边界条件。
    • exceedBound(v + [e]) 函数定义了部分解的有效性标准，如果扩展后的部分解无效，则跳过当前节点 e。
  7. 回溯 backtrack(v)：
    • 如果所有邻接节点都处理完毕或找到一个有效解后，进行回溯操作，即从当前部分解 v 中移除最后一个元素，以便返回到上一步状态。
    • backtrack(v) 函数通常包括从 v 中删除最后一个元素，并可能进行一些其他恢复操作。

简单来说就是通过深度优先搜索暴力地遍历完所有解的空间，期间通过边界检查剪掉不合理的分支缩小查找范围。

回溯法求解数独

有了上面的铺垫，求解数独的问题可以分解为以下流程：

  1. 先判断盘面是否合理，盘面不合理就退出。
  2. 试探性地在未解决的位置填入数字，并考虑下一个未解决的位置。
  3. 如果下一个位置没有任何可填的数字，则回溯到上一个决策点重新决策。
  4. 如果已经没有未解决的位置了，就说明已经找到解了，输出解。

实现之后：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
# 通过回溯法求解数独的解
from typing import List
import sys

# 预处理，先把盘面读进来
board = [["5","3",".",".","7",".",".",".","."], 
         ["6",".",".","1","9","5",".",".","."], 
         [".","9","8",".",".",".",".","6","."], 
         ["8",".",".",".","6",".",".",".","3"], 
         ["4",".",".","8",".","3",".",".","1"], 
         ["7",".",".",".","2",".",".",".","6"], 
         [".","6",".",".",".",".","2","8","."],
         [".",".",".","4","1","9",".",".","5"],
         [".",".",".",".","8",".",".","7","9"]]

n = len(board)

row_counter_list = [set() for _ in range(n)]
col_counter_list = [set() for _ in range(n)]
square_counter_list = [set() for _ in range(n)]

# 待求解的位置
unknown_queue = []

for i in range(n):
    for j in range(n):
        num = board[i][j]
        if num == ".":
            unknown_queue.append((i, j))
            continue
        # 先行后列再方框
        if num in row_counter_list[i]:
            print(f"盘面无效!")
            sys.exit(1)
        else:
            row_counter_list[i].add(num)

        if num in col_counter_list[j]:
            print(f"盘面无效!")
            sys.exit(1)
        else:
            col_counter_list[j].add(num)
        
        row_index = i // 3
        col_index = j // 3
        square_index = row_index * 3 + col_index
        if num in square_counter_list[square_index]:
            print(f"盘面无效!")
            sys.exit(1)
        else:
            square_counter_list[square_index].add(num)


def solve(result: List[List[int]]):
    # 求解函数，result为决策序列
    if len(unknown_queue) == 0:
        # 这里已经找到合适的解了，输出盘面即可
        print(f"求解完成，找到解：")
        for row in range(n):
            print(" ".join(board[row]))
    else:
        # 这里继续求解未知的数
        i, j = unknown_queue[0]
        # 定位对应的counter
        row_counter = row_counter_list[i]
        col_counter = col_counter_list[j]
        square_counter = square_counter_list[i//3 * 3 + j//3]

        for res in range(1, 10):
            str_res = str(res)
            if str_res in row_counter or str_res in col_counter or str_res in square_counter:
                # 剪枝掉不合理的结果
                continue
            
            result.append([i, j, res])
            # 更改盘面
            board[i][j] = str_res
            row_counter.add(str_res)
            col_counter.add(str_res)
            square_counter.add(str_res)
            # 决定后未决策队列出队
            unknown_queue.pop(0)
            # 深度搜索
            solve(result)
        
    # 回溯，这里说明要撤销上一次的决定了
    if len(result) > 0:
        i, j, k = result.pop()
        str_k = str(k)
        # 复原盘面
        row_counter = row_counter_list[i]
        col_counter = col_counter_list[j]
        square_counter = square_counter_list[i//3 * 3 + j//3]

        row_counter.remove(str_k)
        col_counter.remove(str_k)
        square_counter.remove(str_k)

        board[i][j] = "."

        # 插入新求解任务
        unknown_queue.insert(0, (i, j))
    else:
        print("the end...")
    

solve([])

拿wiki上的题目测试一下：

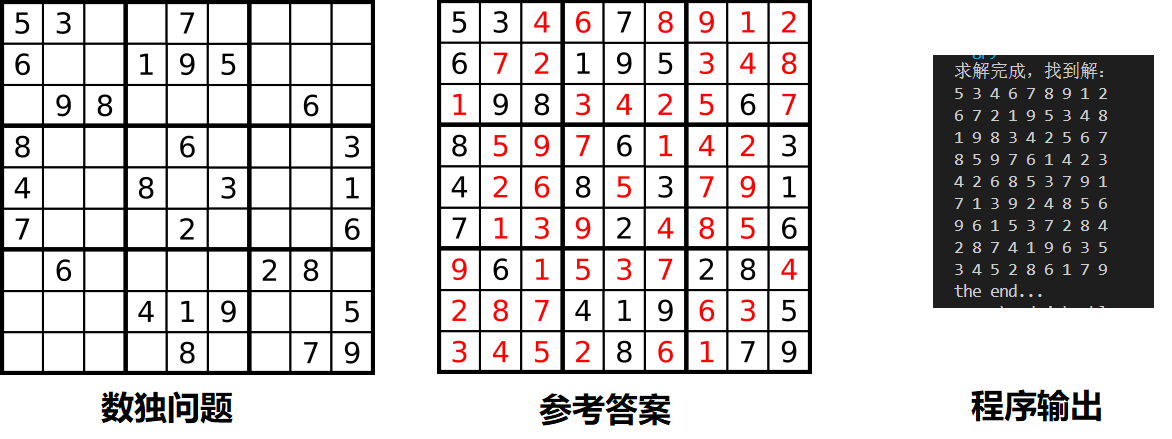
image-20240708140942130

可以发现结果是没问题的，再测试一道题：

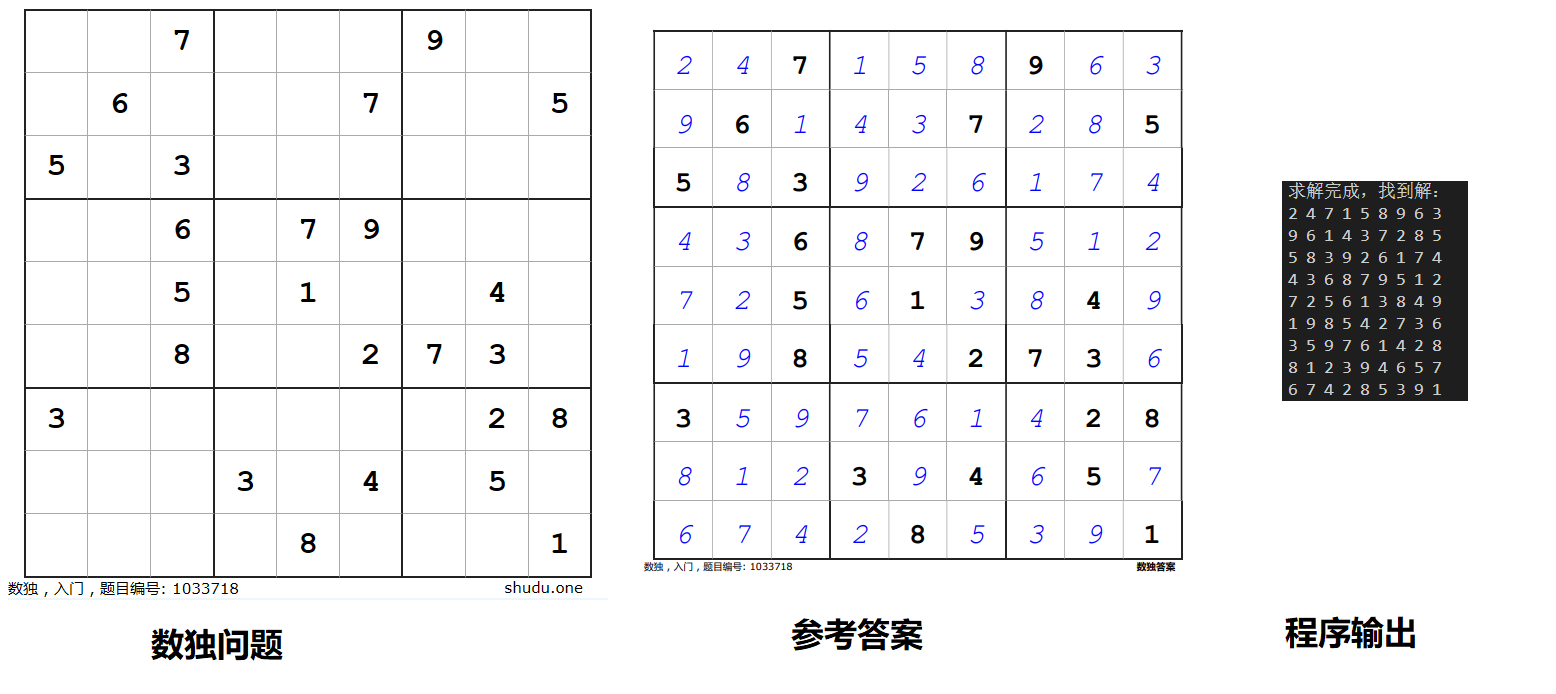
image-20240708141611945

结果也没有问题。

然后这样，用回溯法解决数独问题的程序就写好了。

优化思路

现在的代码已经可以解决数独问题了，但逻辑是通过依次向未知位置试探性填入数字做到的。这里面没有用到盘面的先验信息，每次都从最前面的未知位置开始填，填错了就回溯直到遍历完所有空间。

这显然有点不符合人做数独的逻辑，人做数独肯定是要观察盘面的，不然数独题也不会有入门、简单、困难这样的难度划分。以第一个数独例子来说，如果我们按顺序先填红色箭头的位置，则可以填1，2，4三个数，这里就有3个分支。但如果我们先填蓝色箭头的位置呢？蓝色箭头的位置以及有很多约束条件了，只能填4，只有一个分支，不需要在这里进行回溯了。

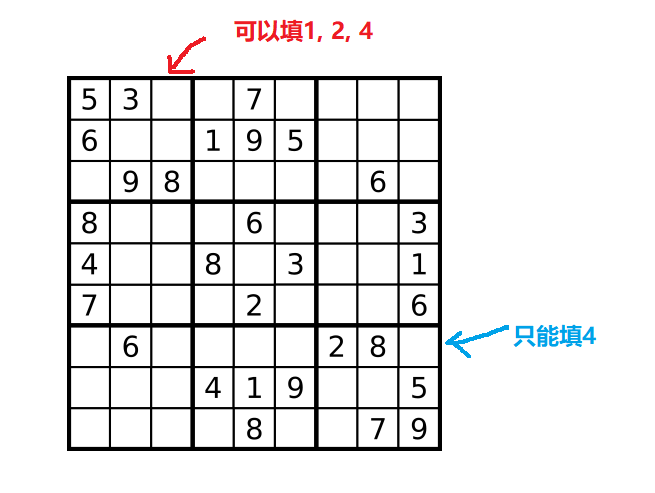
image-20240708143454561

问题就转化为了：如何启发式地选择决策点，使得回溯的次数最少？

这样可以缩小搜索的空间，从而提升算法效率（当然回溯法最坏情况一定是指数的，这里的效率是指的回溯的次数）。

其实可以看出，一个点的难易程度可以用现在可用的解空间描述。可以用一个优先队列来维护盘面信息，以解空间的大小做一个优先队列，优先弹出解空间小的未知位置做决策。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
# 通过回溯法求解数独的解
from typing import List
import sys
import heapq

# 预处理，先把盘面读进来
board = [["5","3",".",".","7",".",".",".","."], 
         ["6",".",".","1","9","5",".",".","."], 
         [".","9","8",".",".",".",".","6","."], 
         ["8",".",".",".","6",".",".",".","3"], 
         ["4",".",".","8",".","3",".",".","1"], 
         ["7",".",".",".","2",".",".",".","6"], 
         [".","6",".",".",".",".","2","8","."],
         [".",".",".","4","1","9",".",".","5"],
         [".",".",".",".","8",".",".","7","9"]]

n = len(board)

row_counter_list = [set() for _ in range(n)]
col_counter_list = [set() for _ in range(n)]
square_counter_list = [set() for _ in range(n)]

# 待求解的位置
unknown_queue = []

# 找到可行解前的回溯次数
backtracing_num = 0

for i in range(n):
    for j in range(n):
        num = board[i][j]
        if num == ".":
            continue
        # 先行后列再方框
        if num in row_counter_list[i]:
            print(f"盘面无效!")
            sys.exit(1)
        else:
            row_counter_list[i].add(num)

        if num in col_counter_list[j]:
            print(f"盘面无效!")
            sys.exit(1)
        else:
            col_counter_list[j].add(num)
        
        row_index = i // 3
        col_index = j // 3
        square_index = row_index * 3 + col_index
        if num in square_counter_list[square_index]:
            print(f"盘面无效!")
            sys.exit(1)
        else:
            square_counter_list[square_index].add(num)

# 这里需要统计完盘面了再进行一次观察
for i in range(n):
    for j in range(n):
        num = board[i][j]
        if num == ".":
            # 计算解空间
            row_index = i // 3
            col_index = j // 3
            square_index = row_index * 3 + col_index
            fs_space = 9 - len(row_counter_list[row_index] | col_counter_list[col_index] | square_counter_list[square_index])
            heapq.heappush(unknown_queue, (fs_space, i, j))
            continue

def solve(result: List[List[int]]):
    # 求解函数，result为决策序列
    global backtracing_num
    if len(unknown_queue) == 0:
        # 这里已经找到合适的解了，输出盘面即可
        print(f"求解完成，找到解：")
        for row in range(n):
            print(" ".join(board[row]))
        print(f"找到可行解前回溯次数: {backtracing_num}")
    else:
        # 这里继续求解未知的数
        fs_space, i, j = unknown_queue[0]
        # 定位对应的counter
        row_counter = row_counter_list[i]
        col_counter = col_counter_list[j]
        square_counter = square_counter_list[i//3 * 3 + j//3]

        for res in range(1, 10):
            str_res = str(res)
            if str_res in row_counter or str_res in col_counter or str_res in square_counter:
                # 剪枝掉不合理的结果
                continue
            
            result.append([fs_space, i, j, res])
            # 更改盘面
            board[i][j] = str_res
            row_counter.add(str_res)
            col_counter.add(str_res)
            square_counter.add(str_res)
            # 决定后未决策队列出队
            heapq.heappop(unknown_queue)
            # 深度搜索
            solve(result)
        
    # 回溯，这里说明要撤销上一次的决定了
    if len(result) > 0:
        backtracing_num += 1
        fs_space, i, j, k = result.pop()
        str_k = str(k)
        # 复原盘面
        row_counter = row_counter_list[i]
        col_counter = col_counter_list[j]
        square_counter = square_counter_list[i//3 * 3 + j//3]

        row_counter.remove(str_k)
        col_counter.remove(str_k)
        square_counter.remove(str_k)

        board[i][j] = "."

        # 插入新求解任务
        heapq.heappush(unknown_queue, (fs_space, i, j))
    else:
        print("the end...")
    

solve([])

主要区别就是通过fs_space变量来考虑初始盘面信息了，先从可填的解少的地方开始填起。

为了比较优化前后的区别，通过backtracing_num来记录找到可行解前的回溯次数。同样求解示例1和示例2，打印优化前后的回溯次数：

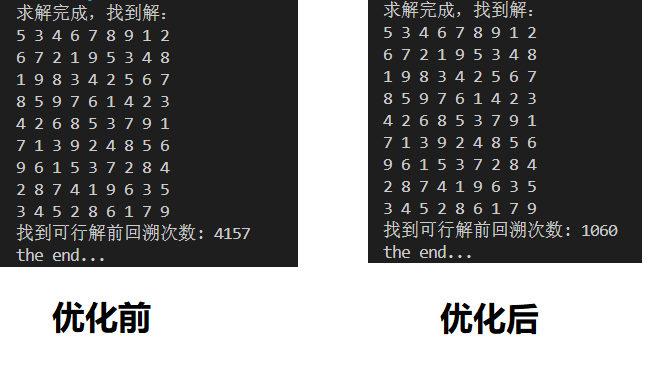
image-20240708150857736
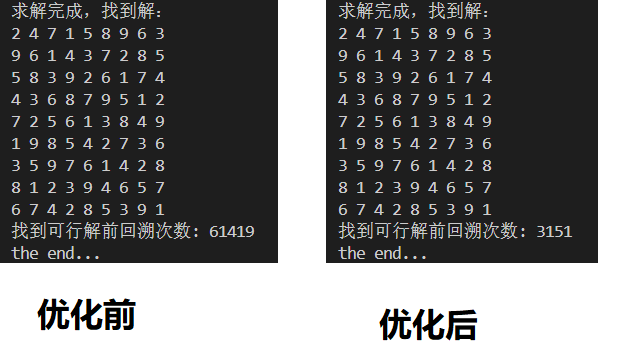
image-20240708151114894

可以看到，对于案例1回溯次数减少到原来的1/4，而案例2则减少到原来的近1/20了。这说明考虑盘面信息先验可以有效地减少回溯的次数。

但代价是什么呢？构建和维护这样的优先队列也是要时间的。但好在构建优先队列大约花费O(nlog n)复杂度，而每次回溯把元素插回去消耗O(log n)复杂度，相比指数复杂度影响不大。（n是待求解元素总数）

也可能会进一步地想，要是每次决策也同时考虑这次决策给其他未求解格子的可行解空间造成影响，动态考虑盘面可不可行呢？应该也是可行的，倒不如说这样更符合人类的决策习惯。但是优先队列一个问题就是插入元素后不好更改优先级，会破坏堆结构内部的顺序。如果不用堆结构，那每次获取待决策位置都会产生开销，这里有点不好。

因此，为了整体结构的简洁性，放弃动态考虑整体盘面，而是直接初始盘面用到最后。

总结

通过数独求解，回顾了回溯法的流程和编程框架。