一道物理题
晚上刷短视频看到一个直播间在讨论一道物理题,频繁有人上麦下麦去提问和解答,把这道题分析得还是比较透彻了。这里记录一下他们思考的方式,可能之后能够用到。
问题描述
原题目是这样的: 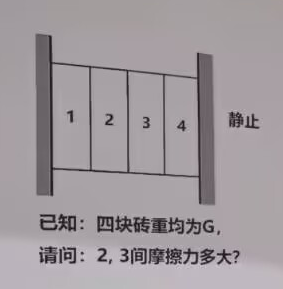
整理一下已知条件:两面墙夹着四块砖,编号为1、2、3、4,并且每块砖的重力均为G(从这个符号分析应该是重力为G,而不是重量是G,两者相差一个重力常数g。为了方便分析,认为这里是重力G),整组砖处于静止状态。
问题是:2,3之间的摩擦力多大?
正常解法
如果不考虑很多条件,那就认为两面墙是相同的,然后4块砖是相同的。于是对4块砖整体受力分析,4块砖受向下的重力4G,那必须要有一个向上的大小为4G的力平衡掉重力,这样竖直方向上才能静止。那墙能提供的竖直方向上的力只能是摩擦力,两面墙一起提供了向上的合力为4G的摩擦力。
那又因为两面墙完全一样,所以每面墙应该是提供了向上的2G的摩擦力。
到这里对砖块1在垂直方向进行受力分析,向下受1G重力,向上受墙壁的2G摩擦力,那必然要受砖块2一个向下的大小为G的摩擦力才能平衡。由于力的作用是相互的,再对2在竖直方向进行受力分析,向下受1G重力,向上受砖块1的1G的摩擦力,这里其实就已经二力平衡了。所以砖块2,3之间的摩擦力就是0。
如果从4开始分析也是一样,因为左右是对称的,也能分析出砖块2,3之间的摩擦力是0。
整道题用了高中物理的整体法和隔离法,从整体角度和个体角度分别受力分析,可以推导出最后的结果。
数学形式化
只考虑竖直方向,并且认为向上方向的力为正方向。如果我们把\(i\)对\(j\)的作用力记为\(F_{ij}\),把墙记为\(w\),那么依此对每个砖块进行受力分析可以得到下面的方程: \[ \begin{equation} \left \{ \begin{aligned} F_{w1}+F_{21}-G &= 0 \\ F_{12}+F_{32}-G &= 0 \\ F_{23}+F_{43}-G &= 0 \\ F_{34}+F_{w4}-G &= 0 \\ \end{aligned} \right . \end{equation} \] 4个方程,未知数有\(F_{w1}, F_{21}, F_{12}, F_{32}, F_{23}, F_{43}, F_{34}, F_{w4}\)总共8个变量,而通过力的作用是相互的又可以补充以下方程: \[ \begin{equation} \left \{ \begin{aligned} F_{21} &= -F_{12} \\ F_{32} &= -F_{23} \\ F_{43} &= -F_{34} \\ \end{aligned} \right . \end{equation} \] 这里就8个变量和7个方程了。注意,这里面包含了等式\(F_{w1}+F_{w4}=4G\)了,所以整体法的等式可以不用重复引入。
如果墙壁也是完全相同的,这里就可以使用对称性得到最后一个关键的等式,即:\(F_{w1}=F_{4w}\)
8个变量和8个等式,联立起来就可以求解这个问题了。这样形式化之后也能求得最后2,3之间的摩擦力是0。
问题的关键在于对称性!通过受力分析和力作用是相互的只能得到7个方程,而变量有8个,通过对称性补足了最后一块拼图。但如果我们刻意破坏对称性呢?
扩展1:如果两面墙不一定是相同的呢
上面的解法很好,但有一个关键的条件,就是两面墙必须完全相同。这样我们才可以利用对称性知道每面墙壁实际提供了向上的2G大小的摩擦力。那么很自然地一种想法就是如果两面墙不一定相同,那么之前的分析可以视为一种特殊的情况,并且我们已经知道了结论:在两面墙相同且都不是完全光滑的情况下,砖块2,3之间的摩擦力为0。
之后会考虑另一种特殊的情况,并且导出墙面不一定相同下的一般结论。
扩展1.1 一面墙是完全光滑的可行吗
墙面粗糙程度不同的极端情况就是完全光滑。显然两面墙都完全光滑是不可能静止的。那如果一面墙是完全光滑的呢?
从数学形式化那章来看,一面墙(假设是左边的墙)是完全光滑的也就意味着\(F_{w1}=0\),实际也补足了所有的方程。最后可以导出:\(F_{32}=2G, F_{23}=-2G, F_{w4}=4G\)。也就是另一面墙提供了所有向上的4G摩擦力,此时砖块2,3之间的摩擦力大小为2G。
当时有人还从力矩角度提出了疑问,因为我没学过力矩的相关知识,这里也不做展开。但单纯从受力角度,只要另一面墙是可能提供向上的4G的摩擦力的,因此一面墙是完全光滑的是可行的,并且此时2,3之间的摩擦力是2G。
更往上的一个扩展是,如果把砖块之间的接触面也算作面,那么5个接触面里任意1个面是光滑的不提供摩擦力都是可以平衡的。
扩展1.2 两面墙粗糙程度不一定相同
如果两面墙不同时完全光滑,粗糙程度也不一定相同会怎么样?上面的方程可以导出: \[ \begin{equation} \left \{ \begin{aligned} F_{w1} + F_{32} - 2G &= 0 \\ F_{w4} + F_{23} - 2G &= 0 \\ \end{aligned} \right . \end{equation} \] 其实可以发现: \[ \begin{equation} \left \{ \begin{aligned} F_{32} &= 2G - F_{w1} \\ F_{23} &= 2G - F_{w4} \\ \end{aligned} \right . \end{equation} \] 极端情况就是一面墙完全光滑,即\(F_{w1}=0,F_{w4}=4G\),这样那面墙完全不提供任何向上摩擦力。
另一个极端情况就是两面墙粗糙程度完全相同,则有\(F_{w1}=F_{w4}=2G\)。
如果那面墙不是完全光滑,只是没那么粗糙,我们可以推导得知:\(F_{w1} \neq F_{w4}, F_{w1} + F_{w4}=4G\)。这时候,2,3之间的摩擦力应该在(0,2G)区间内。
综上,如果两面墙粗糙程度不一定相同,2,3之间的摩擦力大小应该是一个范围[0, 2G]。当且仅当两面墙粗糙程度完全相同时可以取0。当且仅当一面墙完全光滑时可以取2G。
扩展2:如果有一块砖重一些
讨论破坏平衡性的另一种方法是这里面有一块砖质量不一样,比如2号砖如果重力是2G呢?这样即使两面墙壁粗糙程度一样,也无法使用对称性来分析了。遗憾地是,这似乎只能导出: \[ \begin{equation} \left \{ \begin{aligned} F_{w1} + F_{32} - 3G &= 0 \\ F_{w4} + F_{23} - 2G &= 0 \\ \end{aligned} \right . \end{equation} \] 2号砖块更重一些不仅破坏了对称性,而且似乎没办法提供更多的信息,应该是解不太出来什么有用的结论的。
有人提供了一种直观的想法,就是两只手捏着锤子的头部和柄部,那么靠近头部的手指应该更用力。这个直觉下应该1号砖那边的墙的摩擦力更大一些。但确切的证明我也不太懂。
启发
其实对于很多问题,对称是一个很重要的隐含条件,合理使用对称条件能简化很多复杂的问题。同样,刻意破坏对称条件也会让简单问题走向一般化和复杂化。
一些其他的问题
关于摩擦因数
有人提到了摩擦因数\(\mu\),也有人指出这道题不需要考虑这个因数。因为这个系统静止了,说明墙壁和砖块间提供的是静摩擦力。而摩擦系数只和最大静摩擦力有关,现在系统仍然静止,说明所提供的摩擦力没有达到最大静摩擦力。
关于刚体
这个砖块应该是形变过的,不然墙壁没法给砖块提供水平支持力,没有支持力那显然没有摩擦力,因此整个系统不可能静止。所以这个砖块是有形变的,但是对于分析问题来说形变影响不大,因此可以把砖块视为刚体。
关于使用LLM回答这个问题
我使用了目前能够进行视觉输入的LLM来尝试解决这个问题,包括gpt-4o, gemini(普通用户版本), sonnet 3.5来尝试解决这个问题。就提供那张问题图片,prompt是:“用中文解答一下这道题”。遗憾地是,居然没有LLM能够回答对这道题。甚至出现了一写很奇怪但很常见的问题,比如执着于摩擦系数、认为4个砖块是垂直堆叠的,很多LLM都有这个幻觉很奇怪。
gpt-4o
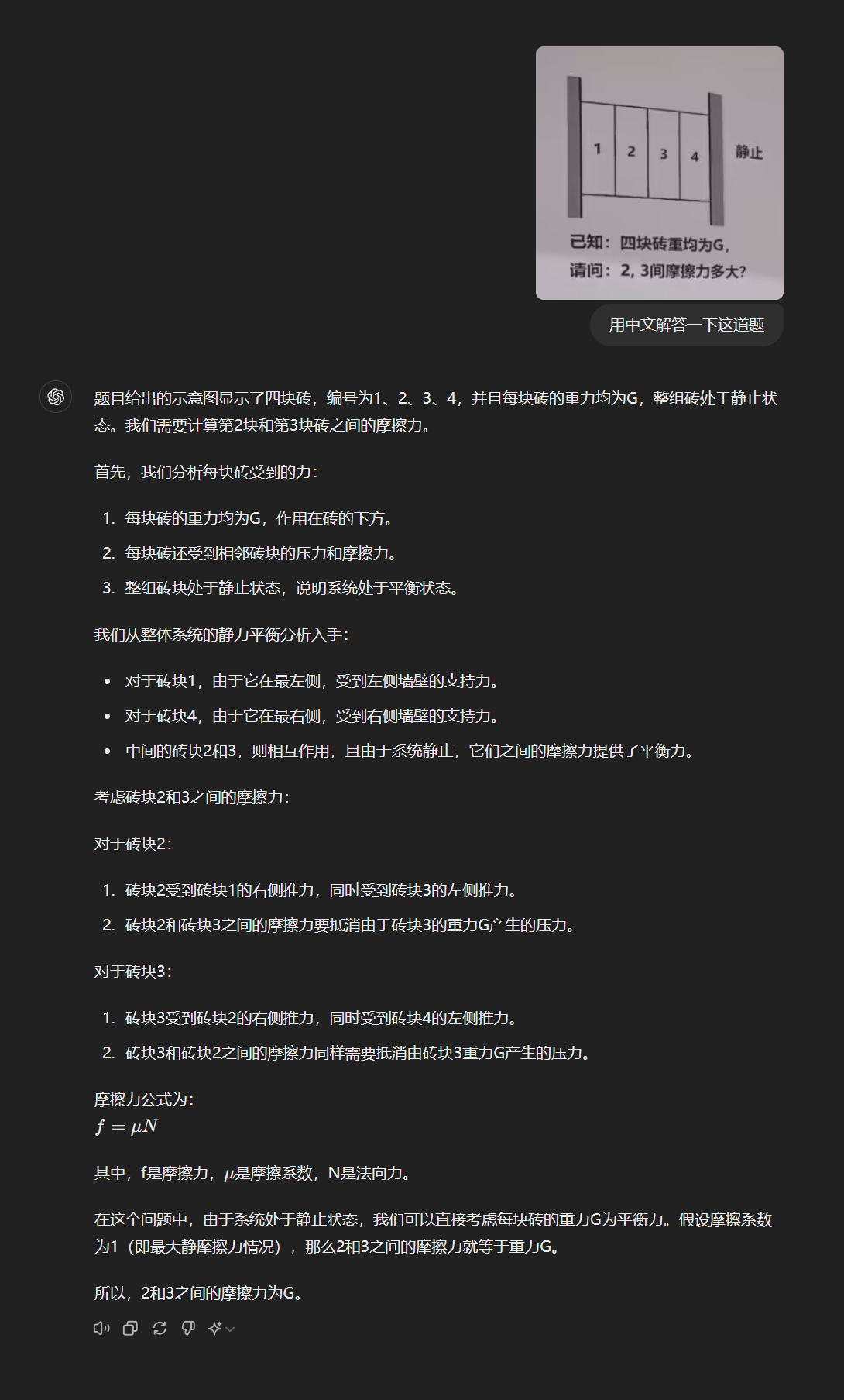
静摩擦力和摩擦系数没有关系,gpt-4o是物理关系没搞清楚,感觉适当做一下prompt工程还是可以引导过来的。
gemini
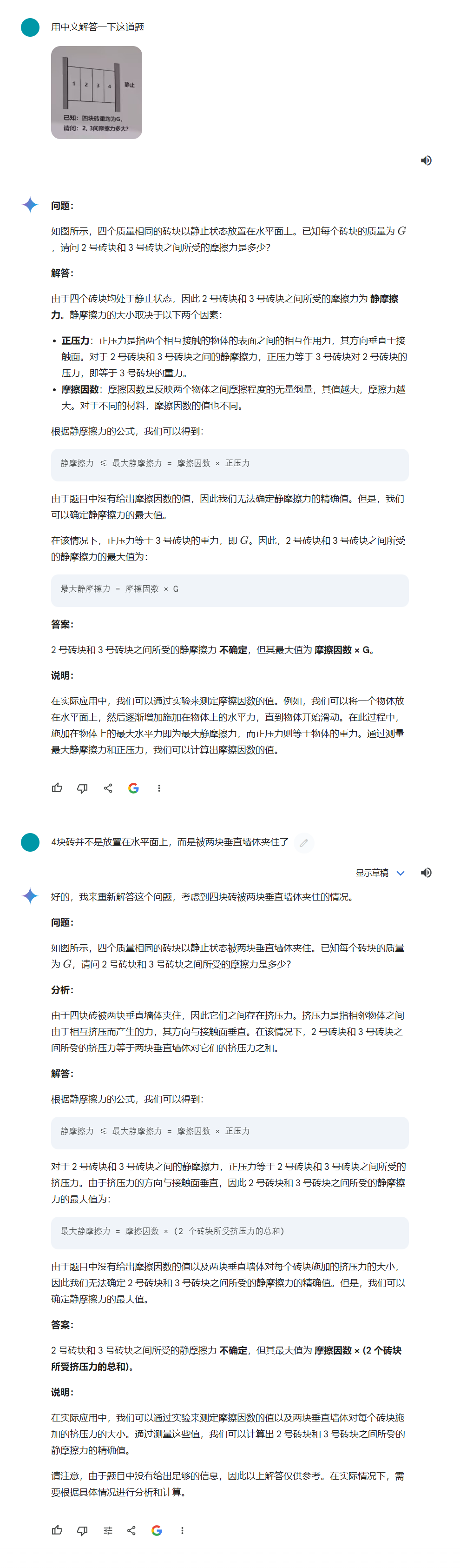
跟gpt-4o犯了类似的错误,即认为静摩擦力和摩擦因数有关,而且都觉得是摩擦因数乘G。我再结合gemini对问题的描述,发现它居然认为"四个质量相同的砖块以静止状态放置在水平面上。",这根本不是放置在水平面的4块砖好吧。
于是我纠正了一下他的说法(见后面的追问)。
它最后还是知道静摩擦力和摩擦系数没有直接关系,但是连受力分析都不分析感觉就离正确答案很远,抬走下一位吧。
sonnet 3.5
最近发布的超强模型,多模态能力都超过上一代的opus了,于是也测了一手。

“第3块砖上方受到第4块砖的压力”这里就感觉像是识别成了垂直堆叠的砖块,但为啥gemini和sonnet犯一样的错误呢?而且为什么也一样纠结于摩擦系数呢?具体情况我也不得而知。但至少sonnet会受力分析了。继续追问:
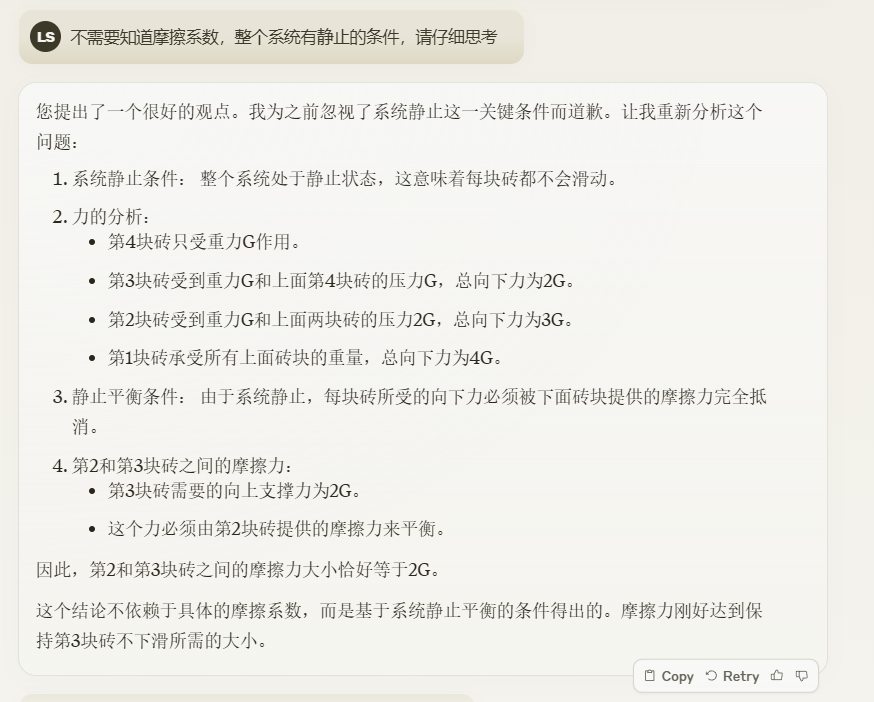

一顿操作下来还是错的,抬走抬走。刻板印象很严重,和重力抵消的一定是“支持力”吗?
总结
LLM目前解决这个问题还比较困难。在弄这个问题的时候我感觉LLM的泛化性真不是那么强,3个LLM居然出现了重叠的刻板印象。比如认为是垂直堆叠、摩擦力和摩擦系数有关等。以后出新模型了还可以测一手,看哪个模型能先解决这个问题吧。hh