sinusoidal简介
简介
自注意力机制是没有位置信息的,即对于元素相同的向量序列,打乱顺序后之前每个元素的输出也依旧不变,这在自然语言里是不合理的。因此需要引入位置编码表征token在序列里的位置。 原始Transformer模型使用了Sinusoidal位置编码,不需要训练而是通过加入正余弦信息来为每个token加入顺序信息。标准的Sinusoidal形式如下: \[ \begin{equation}\left\{\begin{aligned}&p_{k,2i}=\sin(k/10000^{2i/d})\\ &p_{k, 2i+1}=\cos (k/10000^{2i/d} ) \end{aligned}\right. \end{equation} \]
基本思路
假设模型为\(f(⋯,x_m,⋯,x_n,⋯)\),其中标记出来的\(x_m,x_n\)分别表示第m,n个输入,不失一般性,设f是标量函数。对于不带Attention Mask的纯Attention模型,它是全对称的,即对于任意的\(m,n\),都有: \[ \begin{equation} f(\cdots, x_m, \cdots, x_n, \cdots) = f(\cdots, x_n, \cdots, x_m, \cdots) \end{equation} \] 公式(2)即Transformer无法识别位置的原因,函数天然满足\(f(x,y)=f(y,x)\),以至于无法从结果上区分输入的是\([x,y]\)还是\([y,x]\)。 在每个位置上加上一个不同的编码向量: \[ \begin{equation}\tilde{f}(\cdots,x_m,\cdots,x_n,\cdots)=f(\cdots,x_m + p_m,\cdots,x_n + p_n,\cdots)\end{equation} \] 这样原来的对称性就被打破了,加一个位置编码可以用来区分token位置从而处理有序的输入了。
相对位置
泰勒展开之后可发现有一个同时包含\(p_m, p_n\)的交互项,记为\(p_m H p_n\),希望它能表达一定的相对位置信息。
之后假设\(H=I\),那么\(p_m H p_n = p_m p_n = \lang p_m, p_n \rang\),即两个位置编码的内积。希望在这个简单的例子中该项表达的是相对位置信息,即存在某个函数\(g\)使得 \[ \begin{equation} \lang p_m, p_n \rang = g(m-n) \end{equation} \] 解这个方程可以得到正弦位置编码在2维情况下的显式解: \[ \begin{equation} p_m = \begin{pmatrix} \cos m\theta \\ \sin m\theta \end{pmatrix} \end{equation} \] 由于内积满足线性叠加性,所以更高维的偶数维位置编码,我们可以表示为多个二维位置编码的组合: \[ \begin{equation} p_m = \begin{pmatrix} \cos m\theta_0 \\ \sin m\theta_0 \\ \cos m\theta_1 \\ \sin m\theta_1 \\ \vdots \\ \cos m\theta_{d/2-1} \\ \sin m\theta_{d/2-1} \\ \end{pmatrix} \end{equation} \]
远程衰减
基于前面的假设,我们推导出了位置编码的形式(6),它跟标准Sinusoidal位置编码(1)形式基本一样了,只是sin,cos的位置有点不同。一般情况下,神经网络的神经元都是无序的,所以哪怕打乱各个维度,也是一种合理的位置编码,因此除了各个\(θ_i\)没确定下来外,式(6)和式(1)并无本质区别。
式(1)的选择是\(θ_i=10000−2i/d\),这个选择有什么意义呢?事实上,这个形式有一个良好的性质:它使得随着\(|m−n|\)的增大,\(⟨pm,pn⟩\)有着趋于零的趋势。按照我们的直观想象,相对距离越大的输入,其相关性应该越弱,因此这个性质是符合我们的直觉的。
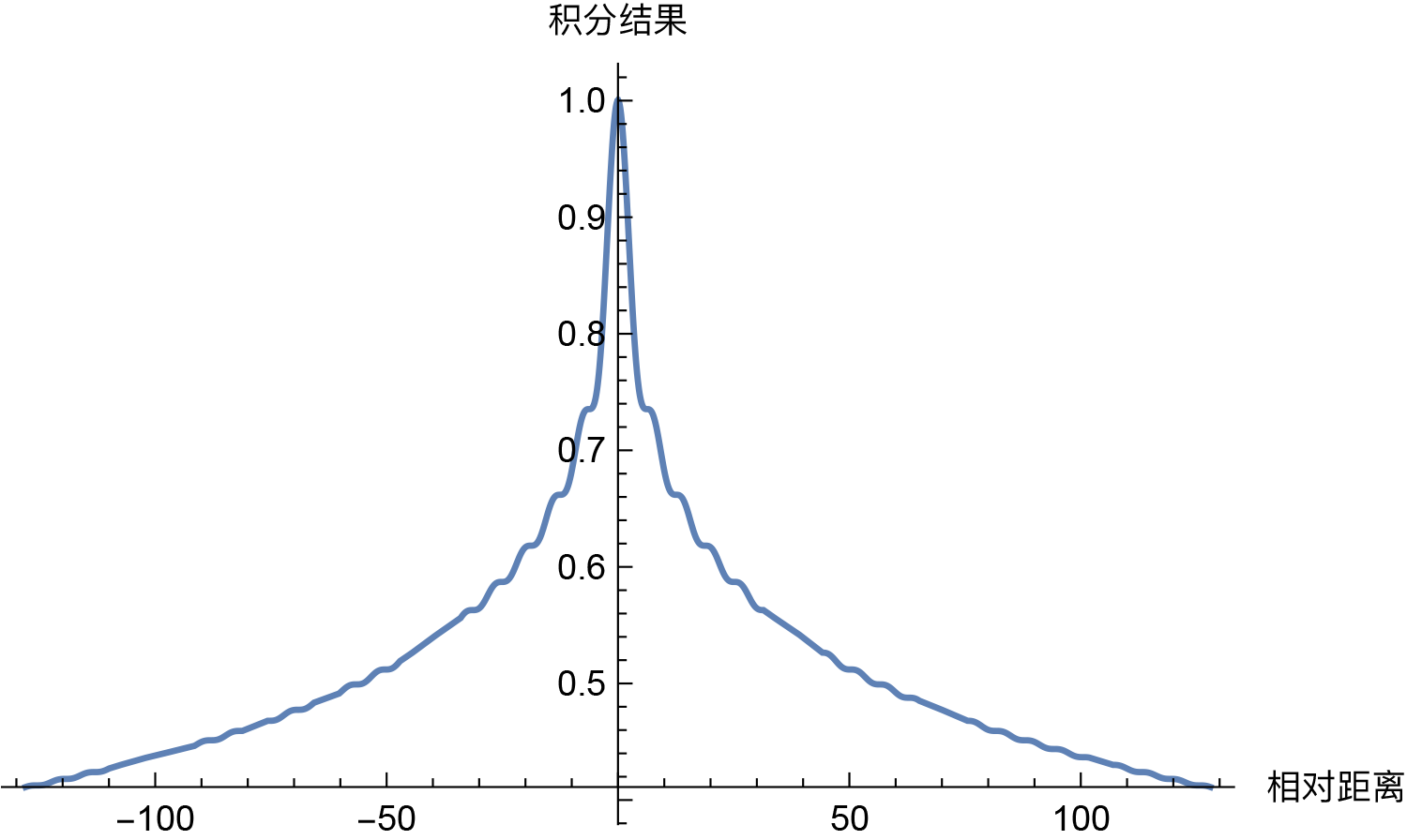
至此,已经导出了正弦位置编码的基本形式。 总结
- 正弦位置编码不需要训练,具有表征位置使得Transformer能区分token顺序的作用。
- 通过泰勒展开得到两个位置编码作用项,使两个位置编码与它们的相对位置产生关系,可以导出正弦位置编码是cos和sin的正余弦三角函数两两一组组成的绝对位置编码。
- 通过分析远程衰减可以导出\(\theta_i = 10000^{-2i/d}\)。