rope简介
简介
旋转位置编码（Rotary Position Embedding，RoPE）是论文Roformer: Enhanced Transformer With Rotray Position Embedding 提出的一种能够将相对位置信息依赖集成到 self-attention 中并提升 transformer 架构性能的位置编码方式。而目前很火的 LLaMA、GLM 模型也是采用该位置编码方式。在RoPE中，出发点就是“通过绝对位置编码的方式实现相对位置编码”。 和相对位置编码相比，RoPE 具有更好的外推性，目前是大模型相对位置编码中应用最广的方式之一。
基本思路
假设通过下述运算来给\(q,k\)添加绝对位置信息： \(\tilde{q}_{m} = f(q,m), \tilde{k}_{m}=f(k,n)\) 经过这个操作之后，\(\tilde{q}_{m}, \tilde{k}_{n}\)就带有位置\(m, n\)的绝对位置信息。Attention的核心运算是内积，所以希望内积的结果带有相对位置信息，假设存在恒等关系： \[ \lang f(q,m)f(k,n) \rang =g(q,k,m-n) \tag{1} \] 求解之后得到如下关系： \[ f(q,m) = \begin{pmatrix} \cos m\theta & -\sin m\theta \\ \sin m\theta & \cos m\theta \end{pmatrix} \begin{pmatrix} q_0 \\ q_1 \end{pmatrix} \tag{2} \] 这个变换实际对应着向量的旋转，即编码后相当于原来的\(q\)旋转\(m\theta\)。 因为公式(1)实际建模的是向量内积的关系，而内积满足线性叠加性，因此任意偶数\(d\)维RoPE，都可以变成\(d/2\)组二维向量进行旋转，即： \[ \begin{pmatrix} \cos m\theta_0 & -\sin m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\ \sin m\theta_0 & \cos m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos m\theta_1 & -\sin m\theta_1 & \cdots & 0 & 0 \\ 0 & 0 & \sin m\theta_1 & \cos m\theta_1 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos m\theta_{d/2-1} & -\sin m\theta_{d/2-1} \\ 0 & 0 & 0 & 0 & \cdots & \sin m\theta_{d/2-1} & \cos m\theta_{d/2-1} \\ \end{pmatrix} \begin{pmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \\ \vdots \\ q_{d-2} \\ q_{d-1} \end{pmatrix} \tag{3} \]
远程衰减
\(\theta_i=10000^{-2i/d}\)从而带来一定的远程衰减性。
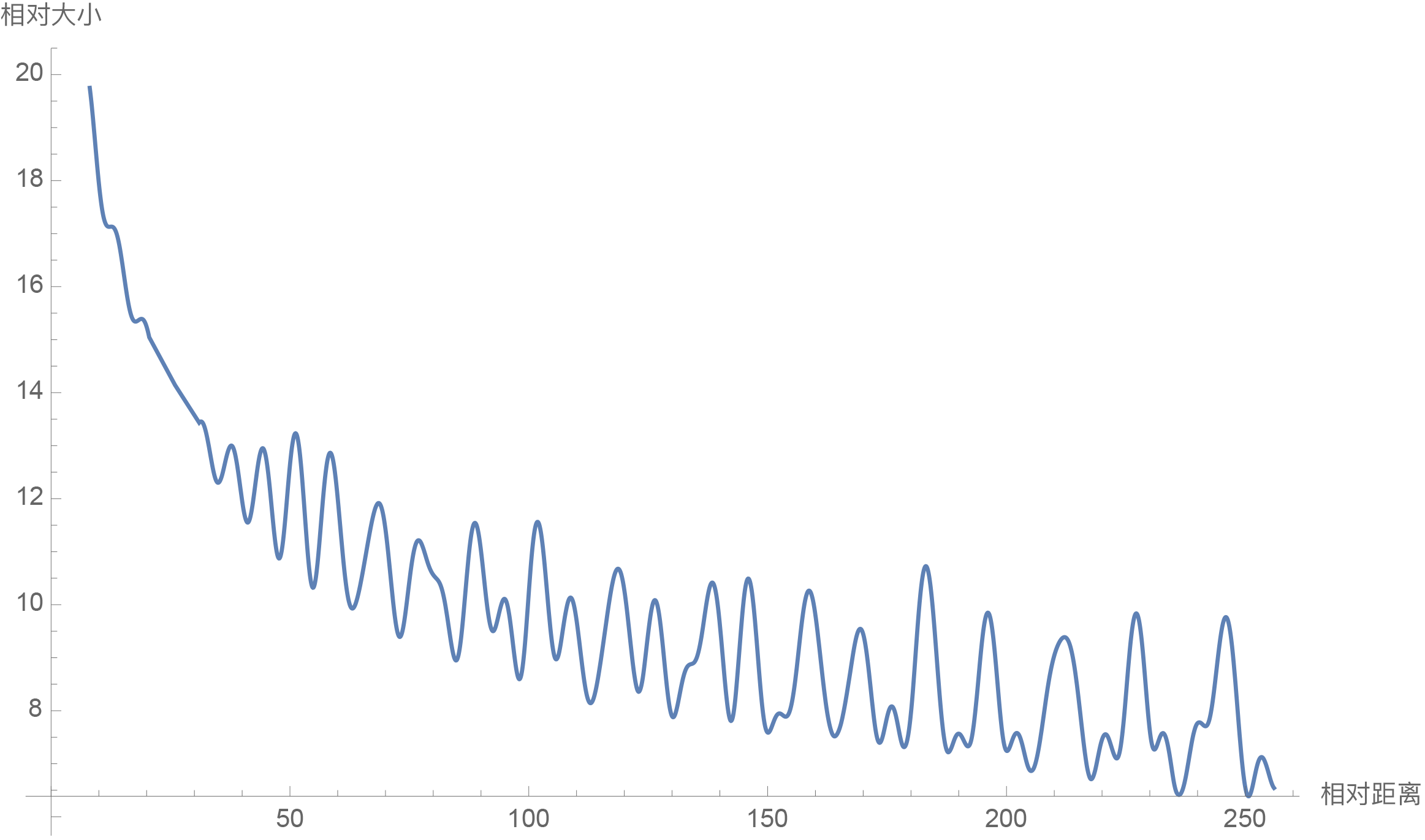从图中我们可以看到随着相对距离的变大，内积结果有衰减趋势的出现。
高效实现
因为旋转矩阵非常稀疏，因此直接用矩阵乘法实现会很浪费算力。可以使用逐元素点乘来实现： \[ \begin{pmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \\ \vdots \\ q_{d-2} \\ q_{d-1} \end{pmatrix} \otimes \begin{pmatrix} \cos m\theta_0 \\ \cos m\theta_0 \\ \cos m\theta_1 \\ \cos m\theta_1 \\ \vdots \\ \cos m\theta_{d/2-1} \\ \cos m\theta_{d/2-1} \\ \end{pmatrix} + \begin{pmatrix} -q_1 \\ q_0 \\ -q_3 \\ q_2 \\ \vdots \\ -q_{d-1} \\ q_{d-2} \end{pmatrix} \otimes \begin{pmatrix} \sin m\theta_0 \\ \sin m\theta_0 \\ \sin m\theta_1 \\ \sin m\theta_1 \\ \vdots \\ \sin m\theta_{d/2-1} \\ \sin m\theta_{d/2-1} \\ \end{pmatrix} \tag{4} \]
特性总结
- 旋转编码RoPE配合Attention机制可以有效地保持位置信息的相对关系，即相邻位置的编码之间有一定的相似性，而远离位置的编码之间有一定的差异性。这样可以增强模型对位置信息的感知和利用。这一点是其他绝对位置编码方式（如正弦位置编码、学习的位置编码等）所不具备的，因为它们只能表示绝对位置，而不能表示相对位置。
- 旋转编码RoPE可以通过旋转矩阵来实现位置编码的外推，即可以通过旋转矩阵来生成超过预训练长度的位置编码。这样可以提高模型的泛化能力和鲁棒性。这一点是其他固定位置编码方式（如正弦位置编码、固定相对位置编码等）所不具备的，因为它们只能表示预训练长度内的位置，而不能表示超过预训练长度的位置。（这一点存疑，很奇怪）
1 | rope的外推能力优于Sinusoidal吗？还是说理论上相对位置编码的外推性都是差不多的？ |