BM 45 滑动窗口的最大值

url：牛客 BM45

最开始做这道题的时候我想着一个窗口里求最大值应该是没啥捷径的，就在窗口里比最大值即可。然后滑动之后就需要观察上一次的最后一个元素是不是上一个窗口的最大值，如果不是的话，就把上个窗口的最大值和当前窗口的第一个值比对，哪个大哪个就是当前窗口的最大值。如果是的话，那这个窗口的最大值就需要重新算。

实现的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#
# 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
#
# 
# @param num int整型一维数组 
# @param size int整型 
# @return int整型一维数组
#
class Solution:
    def maxInWindows(self , num: List[int], size: int) -> List[int]:
        # write code here
        if len(num)==0 or size==0 or len(num) < size:
            return None
        
        result = []
        for i in range(len(num)-size+1):
            if len(result) == 0:
                result.append(max(num[i: i+size]))
            else:
                prev_window_max = result[-1]
                prev_val = num[i-1]
                if prev_val != prev_window_max:
                    if prev_window_max >= num[i+size-1]:
                        result.append(prev_window_max)
                    else:
                        result.append(num[i+size-1])
                else:
                    result.append(max(num[i: i+size]))
        return result

这个是可以通过的。但是题解里面提到了用什么优先队列，而且似乎时间复杂度更好。我感觉有点懵。

有人提到去看leetcode的题解，于是我就去Leetcode里找到了这个题目：Leetcode 239 滑动窗口最大值

改了一下变量名，提交了果然Leetcode里面就过不了，超时了。之后想着应该是移除掉窗口里最大值之后要重新计算最大值很伤，记录次大值应该能缓解这个问题。但思考了一下，如果size是1啥的，这个次大值还得额外作为一个分支维护，很麻烦。

然后我就开始看优先队列的解法，之后发现看得迷迷糊糊的。后面查了资料原来优先队列是基于堆的，正好堆排序啥的已经忘得差不多了，借此机会也重新熟悉一下数据结构——堆。

堆

堆的定义

首先堆一定是一颗完全二叉树，完全二叉树的定义是：若二叉树的深度为 h，除第 h 层外，其它各层的结点数都达到最大个数，第 h 层所有的叶子结点都连续集中在最左边，这就是完全二叉树（第 h 层可能包含 [1~2h] 个节点）。

完全二叉树通俗来理解就是二叉树最后一层可以不是满的，但所有节点都必须靠左排列。这提供了一个重要性质，就是知道层序遍历就可以重建这棵树，这为后面使用数组来表示这个完全二叉树奠定基础。使用数组而不是节点的left和right指针访问二叉树还带来一个好处，就是可以通过子节点位置访问父节点，而无需引入任何额外表示。比如位置是\(k\)的节点其父节点的位置为\(\lfloor \frac{k-1}{2} \rfloor\)。同样如果知道父节点位置为\(i\)，则两个子节点的位置为\(2i+1\)和\(2i+2\)。

接下来来介绍堆的有序性。根据父节点和两个子节点的关系，可以分为大根堆和小根堆。顾名思义，前者就是根节点大于左右子节点，后者就是根节点小于左右子节点。如下图所示：

实际上大根堆和小根堆效果是类似的，只是比较的方向不同而已。为了简单起见，采用《算法（第4版）》堆有序的定义（即大根堆定义）。

堆有序：当一颗二叉树的每个节点都大于等于它的两个子节点时，它被称为堆有序

此时，根节点应该时堆有序的二叉树中的最大节点。

知道了完全二叉树和堆有序的概念之后，可以导出堆的概念了：

堆：堆是一组能够用堆有序的完全二叉树排序的元素，并在数组中按层次遍历顺序储存。

堆的核心操作

从定义我们可以知道堆的特征就是根元素最大，然后每个子树都满足根元素大于左右子树节点，并且堆构成的二叉树是完全二叉树。我们接下来介绍堆的两个核心操作：上浮（自底向下的堆有序化）和下沉（由上至下的堆有序化），通过这两个核心操作我们可以实现向堆中插入元素和弹出堆中最大元素（弹出后保持剩余元素仍然满足堆定义）。

堆有序化：对堆进行一些简单的改动，打破堆的状态，然后再遍历堆并按照要求将堆的状态恢复。

上浮 自底向下的堆有序化

如果堆的有序状态因为某个节点变得比它的父节点更大而打破，那么就需要通过交换它和它的父节点来修复堆。交换之后这个节点仍然可能比它的父节点更大，那我们就重复这个过程知道它浮到合适的位置。代码为：

1
2
3
4
5
6
7
8
9
10
def swim(nums: List[int], k: int):
    # 如果已经浮到顶了就退出
    if k == 0:
        return None
    
    # 比较目标节点和它的父节点
    if nums[k] > nums[(k-1)//2]:
        # 交换父子节点并进入下一轮比较
        nums[k], nums[(k-1)//2] = nums[(k-1)//2], nums[k]
        swim(nums, (k-1)//2)

下沉 由上至下的堆有序化

如果堆的有序状态被某个节点变得比它的两个子节点或是其中之一更小而被打破了，那么可以将它和它的两个子节点中较大者交换来恢复堆。交换之后该节点可能比子节点的子节点还小，重复这个过程直到这个节点比子节点都大或者沉到最底层。代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def sink(nums: List[int], k: int, N=None):
    N = len(nums) if N is None else N
    # 获取左右子节点位置
    left_node_pos = 2*k + 1
    right_node_pos = 2*k + 2
    
    if right_node_pos < N:
        # 这里是左右子节点都在，正常比较即可
        if nums[left_node_pos] > nums[right_node_pos] and nums[left_node_pos] > nums[k]:
            nums[left_node_pos], nums[k] = nums[k], nums[left_node_pos]
            sink(nums, left_node_pos, N)
        elif nums[right_node_pos] > nums[k]:
            nums[right_node_pos], nums[k] = nums[k], nums[right_node_pos]
            sink(nums, right_node_pos, N)
    elif left_node_pos < N:
        # 这里是只有左节点
        if nums[left_node_pos] > nums[k]:
            nums[left_node_pos], nums[k] = nums[k], nums[left_node_pos]
            sink(nums, left_node_pos, N)
    # 如果左右子节点都没有那就是沉到底了，不管了

实现了上浮和下沉后，我们可以实现插入元素和删除最大元素了。

插入元素

插入元素首先是不要破坏堆里完全二叉树的结构，其次是要将插入的元素上浮到合理位置。要想不破坏原来二叉树结构很简单，直接在数组末尾新增一个位置放新元素即可，之后通过上浮操作将新元素交换到合理位置。

1
2
3
4
5
def insert_to_maxHeap(nums: List[int], node: int):
    N = len(nums)
    nums.append(node)
    # 上浮到合理位置
    swim(nums, N)

弹出堆顶元素（弹出最大元素）

同样，弹出堆顶元素也要同时保证弹出后树仍然是完全二叉树，而且剩下的元素都在合理位置。可以将最底层最后的元素与根节点交换位置，并弹出根节点。此时将新的根节点通过下沉操作重新将堆有序化即可。

1
2
3
4
5
6
7
def pop_max_val(nums: List[int]):
    N = len(nums)
    nums[0], nums[N-1] = nums[N-1], nums[0]
    target = nums.pop()
    if len(nums) > 0:
    	sink(nums, 0)
    return target

上浮只需要不超过\(\log_2 N +1\)次的比较，而下沉需要不超过\(2\log_2N\)次的比较。后面的插入元素和弹出元素都依赖于上浮或下沉，因此这4种操作的时间复杂度均为\(O(\log N)\)。

堆的构造和堆排序

堆的构造

如果由N个给定元素构造一个堆有什么高效的方法吗？

一种方法是先构建一个空堆，然后将N个元素依次插入堆中，每次插入最坏需要\(O(\log N)\)的复杂度，要插入N次，总复杂度为\(O(N\log N)\)。

另一种方法是从右到左使用下沉来构造子堆。因为如果左右子树都已经是堆了，那堆父节点使用下沉操作就可以将这棵树变为堆。之后，这棵树又可以作为新的已经堆有序的子树，对父节点的父节点使用下沉操作形成一个新堆。这种方法的妙处在于堆大小是1，也即没有子节点的元素都可以跳过！父节点的位置为\(i\)的话，两个子节点的位置分别为\(2i+1\)和\(2i+2\)，假设\(2i+1\)位置超过数组长度，那么第\(i\)个位置的节点可以跳过。这意味着有一半左右的节点是可以跳过的，只需要对位置不超过\(\lfloor \frac{N}{2} \rfloor\)的元素调用下沉方法即可。但注意要从右向左执行这个操作，因为我们要优先保证执行下沉时左右子树都已经是堆了。当然，我们也可以粗略地计算一些复杂度，对\(\frac{N}{2}\)个元素执行下沉操作，下沉操作最坏需要\(O(\log N)\)的复杂度，因此总复杂度也为\(O(N \log N)\)。虽然复杂度没有改善，但是从上面的讨论也可以知道这种方法比前一种需要比较的元素更少，更加高效。

后一种方法的Python实现如下：

1
2
3
4
5
6
def build_heap(nums: List[int]):
    '''根据任意给定的数组nums构建堆'''
    pos = len(nums) // 2
    while pos >= 0:
        sink(nums, pos)
        pos -= 1

堆排序

堆的构造过程中，将无序的数组变得堆有序了。那现在依次调用删除最大元素的方法把元素从右到左地取出来，就可以对整个数组完成排序了。堆的构造需要\(O(N\log N)\)的复杂度，删除最大元素每次需要\(O(\log N)\)，要操作N次，复杂度也为\(O(N \log N)\)。因此堆排序的复杂度为\(O(N \log N)\)。

我们可以实现这样的操作：

1
2
3
4
5
6
7
8
9
def sort_by_heap_v0(nums: List[int]):
    '''堆排序，先构建堆，之后依次弹出'''
    build_heap(nums)
    result = [-1 for i in range(len(nums))]
    pos = len(nums) - 1
    while pos >= 0:
        result[pos] = pop_max_val(nums)
        pos -= 1
    return result

当然，要新申请一个result数组很扎眼。我们可以思考一件事，就是从长度为\(N\)堆有序的数组里弹出一个元素时，这个元素恰好是排序好的数组中的第\(N\)个元素。也就是说如果我们在删除最大元素时将最大元素移到末尾，实际上已经把这个元素放到正确的位置上了。这时候只需要对被交换上去的元素进行下沉操作，然后收缩堆的范围，就已经排好一个元素并保持了前\(N-1\)个元素的堆有序状态了。我们实现一下这个操作（下沉排序）：

1
2
3
4
5
6
7
8
9
def sort_by_heap(nums: List[int]):
    '''堆排序，但在原数组上完成操作'''
    build_heap(nums)
    pos = len(nums) - 1
    while pos > 0:  # 剩一个数时实际已经完成排序了
        nums[0], nums[pos] = nums[pos], nums[0]
        sink(nums, 0, pos)  # 只需要下沉数组的前N-1个数了
        pos -= 1
	return nums

堆排序的测试代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
from typing import List
def sink(nums: List[int], k: int, N=None):
    N = len(nums) if N is None else N
    # 获取左右子节点位置
    left_node_pos = 2*k + 1
    right_node_pos = 2*k + 2
    
    if right_node_pos < N:
        # 这里是左右子节点都在，正常比较即可
        if nums[left_node_pos] > nums[right_node_pos] and nums[left_node_pos] > nums[k]:
            nums[left_node_pos], nums[k] = nums[k], nums[left_node_pos]
            sink(nums, left_node_pos, N)
        elif nums[right_node_pos] > nums[k]:
            nums[right_node_pos], nums[k] = nums[k], nums[right_node_pos]
            sink(nums, right_node_pos, N)
    elif left_node_pos < N:
        # 这里是只有左节点
        if nums[left_node_pos] > nums[k]:
            nums[left_node_pos], nums[k] = nums[k], nums[left_node_pos]
            sink(nums, left_node_pos, N)
    # 如果左右子节点都没有那就是沉到底了，不管了

def build_heap(nums: List[int]):
    '''根据任意给定的数组nums构建堆'''
    pos = len(nums) // 2
    while pos >= 0:
        sink(nums, pos)
        pos -= 1

def sort_by_heap(nums: List[int]):
    '''堆排序，但在原数组上完成操作'''
    build_heap(nums)
    pos = len(nums) - 1
    while pos > 0:  # 剩一个数时实际已经完成排序了
        nums[0], nums[pos] = nums[pos], nums[0]
        sink(nums, 0, pos)  # 只需要下沉数组的前N-1个数了
        pos -= 1
    return nums


a = [9, 7, 5, 6, 4, 3, 1, 2, 8]
sort_by_heap(a)
print(a)
# result: [1, 2, 3, 4, 5, 6, 7, 8, 9]

用Python实现一个堆

综合上述代码，并且使用面向对象的方式可以自己实现一个堆。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
# 大根堆实现
class MaxHeap:
    def __init__(self, nums=None):
        self.nums = [] if nums is None else nums
        if len(self.nums) > 0:
            self.build_heap()
        
    def build_heap(self):
        pos = len(self.nums) // 2
        while pos >= 0:
            self.sink(pos)
            pos -= 1

    def swim(self, k: int):
        if k > 0 and self.nums[k] > self.nums[(k-1)//2]:
            # 交换父子节点并进入下一轮比较
            self.nums[k], self.nums[(k-1)//2] = self.nums[(k-1)//2], self.nums[k]
            self.swim((k-1)//2)

    def sink(self, k:int, N=None):
        N = len(self.nums) if N is None else N
        # 获取左右子节点位置
        left_node_pos = 2*k + 1
        right_node_pos = 2*k + 2

        if right_node_pos < N:
            # 这里是左右子节点都在，正常比较即可
            if self.nums[left_node_pos] > self.nums[right_node_pos] and self.nums[left_node_pos] > self.nums[k]:
                self.nums[left_node_pos], self.nums[k] = self.nums[k], self.nums[left_node_pos]
                self.sink(left_node_pos, N)
            elif self.nums[right_node_pos] > self.nums[k]:
                self.nums[right_node_pos], self.nums[k] = self.nums[k], self.nums[right_node_pos]
                self.sink(right_node_pos, N)
        elif left_node_pos < N:
        # 这里是只有左节点
            if self.nums[left_node_pos] > self.nums[k]:
                self.nums[left_node_pos], self.nums[k] = self.nums[k], self.nums[left_node_pos]
                self.sink(left_node_pos, N)
        # 如果左右子节点都没有那就是沉到底了，不管了

    def insert(self, node):
        N = len(self.nums)
        self.nums.append(node)
        # 上浮到合理位置
        self.swim(N)
    
    def pop(self):
        N = len(self.nums)
        self.nums[0], self.nums[N-1] = self.nums[N-1], self.nums[0]
        target = self.nums.pop()
        if len(self.nums) > 0:
            self.sink(0)
        return target

堆的应用——优先队列

可以借助堆来实现优先队列。优先队列有两个具体操作：

  1. 插入元素到队列
  2. 弹出最小元素

可以用小根堆来实现。

堆的FQA

本部分来自《算法（第4版）》的优先队列章节的答疑部分。

Q: 为什么要使用堆结构？为什么我们不直接把元素排序然后再一个个引用有序数组中的元素？

A: 在某些数据处理的例子中，数据总量很大，无法排序甚至无法装进内存。如果我们需要从10亿个元素中选出最小的10个，那么对这个数组排序显然不是好办法，但有了堆，就可以每次删除最大的元素并加入新元素即可。

Q: 在堆排序中构造堆时，逐个向堆中添加元素比由底向上的复杂方法更简单。为什么要这么做？

A: 对于一个排序算法来说，这么做能够快上 20%，而且所需的代码更少（不会用到 swim 函数）。理解算法的难度并不一定与它的简洁性或者效率相关。

Q: 在Python中使用堆/优先队列需要自己实现上述操作吗？

A: 实际不需要，因为Python内置了heapq库来完成堆的操作。具体用例如下：

用heapq进行堆排序：

1
2
3
4
5
6
7
def heapsort(iterable):
    h = []
    for value in iterable:
        heappush(h, value)
    return [heappop(h) for i in range(len(h))]

heapsort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0])

借助heapq实现优先队列，甚至通过一个字典使其支持移除任务：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
pq = []                         # list of entries arranged in a heap
entry_finder = {}               # mapping of tasks to entries
REMOVED = '<removed-task>'      # placeholder for a removed task
counter = itertools.count()     # unique sequence count

def add_task(task, priority=0):
    'Add a new task or update the priority of an existing task'
    if task in entry_finder:
        remove_task(task)
    count = next(counter)
    entry = [priority, count, task]
    entry_finder[task] = entry
    heappush(pq, entry)

def remove_task(task):
    'Mark an existing task as REMOVED.  Raise KeyError if not found.'
    entry = entry_finder.pop(task)
    entry[-1] = REMOVED

def pop_task():
    'Remove and return the lowest priority task. Raise KeyError if empty.'
    while pq:
        priority, count, task = heappop(pq)
        if task is not REMOVED:
            del entry_finder[task]
            return task
    raise KeyError('pop from an empty priority queue')

回到BM 45

那有了堆的知识，我们可以用大根堆完成寻找滑动窗口最大值。需要注意的是，大根堆加入元素和弹出最大元素是\(O(\log n)\)的复杂度的，但是要删除某个特定的元素却需要遍历整颗树，即\(O(n)\)复杂度。所以当滑动窗口移动时，并不好直接删除移出滑动窗口的元素。我们可以借鉴heapq中移除任务的方法，对移出滑动窗口的元素进行标记，如果是已经移除了的，就丢掉再pop一次，直到获得滑动窗口内的最大值。用下标能很快判断该元素是否在滑动窗口内，因此我们创建一个包装类，该类比较大小采用value字段比较大小，而附带一个index字段用来记录原来的位置。

1
2
3
4
5
6
7
8
class WrapItem:
    def __init__(self, value, index):
        self.value = value
        self.index = index
    
    def __lt__(self, other: WrapItem):
        # 实现less than方法用于比较对象大小
        return self.value < other.value

组合上面的大根堆和本章的包装类，就可以出来解决方案了。完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
#
# 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
#
# 
# @param num int整型一维数组 
# @param size int整型 
# @return int整型一维数组
#

class Solution:
    class WrapItem:
        def __init__(self, value, index):
            self.value = value
            self.index = index
        
        def __lt__(self, other):
            return self.value < other.value
    
    class MaxHeap:
        def __init__(self, nums=None):
            self.nums = [] if nums is None else nums
            if len(self.nums) > 0:
                self.build_heap()
            
        def build_heap(self):
            pos = len(self.nums) // 2
            while pos >= 0:
                self.sink(pos)
                pos -= 1

        def swim(self, k: int):
            if k > 0 and self.nums[k] > self.nums[(k-1)//2]:
                # 交换父子节点并进入下一轮比较
                self.nums[k], self.nums[(k-1)//2] = self.nums[(k-1)//2], self.nums[k]
                self.swim((k-1)//2)

        def sink(self, k:int, N=None):
            N = len(self.nums) if N is None else N
            # 获取左右子节点位置
            left_node_pos = 2*k + 1
            right_node_pos = 2*k + 2

            if right_node_pos < N:
                # 这里是左右子节点都在，正常比较即可
                if self.nums[left_node_pos] > self.nums[right_node_pos] and self.nums[left_node_pos] > self.nums[k]:
                    self.nums[left_node_pos], self.nums[k] = self.nums[k], self.nums[left_node_pos]
                    self.sink(left_node_pos, N)
                elif self.nums[right_node_pos] > self.nums[k]:
                    self.nums[right_node_pos], self.nums[k] = self.nums[k], self.nums[right_node_pos]
                    self.sink(right_node_pos, N)
            elif left_node_pos < N:
            # 这里是只有左节点
                if self.nums[left_node_pos] > self.nums[k]:
                    self.nums[left_node_pos], self.nums[k] = self.nums[k], self.nums[left_node_pos]
                    self.sink(left_node_pos, N)
            # 如果左右子节点都没有那就是沉到底了，不管了

        def insert(self, node):
            N = len(self.nums)
            self.nums.append(node)
            # 上浮到合理位置
            self.swim(N)
        
        def pop(self):
            N = len(self.nums)
            self.nums[0], self.nums[N-1] = self.nums[N-1], self.nums[0]
            target = self.nums.pop()
            if len(self.nums) > 0:
                self.sink(0)
            return target
        
        def getMax(self):
            return self.nums[0]

    def maxInWindows(self , num: List[int], size: int) -> List[int]:
        # write code here
        # 去除边界条件
        if len(num) == 0 or size == 0 or len(num) < size:
            return []
        # 初始化大根堆
        heap = Solution.MaxHeap([Solution.WrapItem(v, i) for i, v in enumerate(num[:size])])
        result = [heap.getMax().value]
        # 向前移动直到完成
        for i in range(size, len(num)):
            # 加入新的节点
            heap.insert(Solution.WrapItem(num[i], i))
            # 取出最大值
            target = heap.getMax()
            # 过滤掉不在窗口内的最大值
            while target.index < i-size+1:
                heap.pop()
                target = heap.getMax()
            # 加入结果中
            result.append(target.value)
        return result

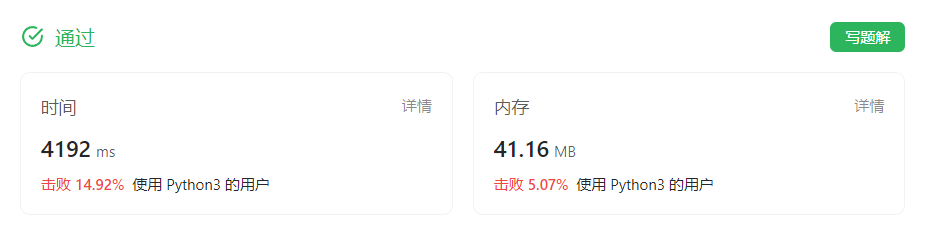
稍微改改参数，可以通过leetcode上239题的提交了。提交的结果为：

image-20230825163054303

我们也可以用Python内置的heapq使用更少的代码完成提交：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import heapq
#
# 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
#
# 
# @param num int整型一维数组 
# @param size int整型 
# @return int整型一维数组
#

class Solution:
    def maxInWindows(self , num: List[int], size: int) -> List[int]:
        # write code here
        # 去除边界条件
        if len(num) == 0 or size == 0 or len(num) < size:
            return []
        # 初始化堆，注意heapq的默认实现为小根堆，因此加入时值乘-1当作大根堆用
        heap = [(-1 * v, i) for i, v in enumerate(num[:size])]
        heapq.heapify(heap)
        result = [heap[0][0] * -1]
        # 步进，直到滑动完
        for i in range(size, len(num)):
            # 加入新节点
            heapq.heappush(heap, (-1 * num[i], i))
            target = heap[0]
            while target[1] < i-size+1:
                heapq.heappop(heap)
                target = heap[0]
            result.append(target[0] * -1)
        return result

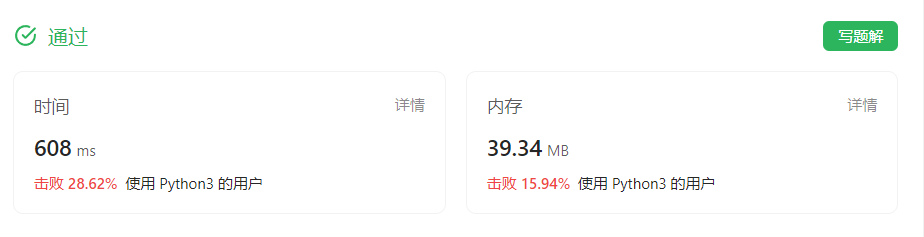
代码简洁很多很多了！而且根据Leetcode上的提交结果也变快变得更省内存了。

image-20230825164727332

时间从4192ms到608ms，还挺夸张的，而且heapq也是纯Python实现，内存方面倒是没有太大不同。时间上的差距应该是我在实现堆的时候用了递归方法而不是非递归循环，这里对性能影响可能比较大。

小结

Anyway, 总算是给这章写完了。小结一下学到的东西吧：

  1. 堆是一种插入和弹出最大/最小元素高效的结构，是优先队列的基础数据结构。
  2. 堆的两个核心操作是上浮和下沉，借助这两个核心操作我们可以高效地向堆中插入元素和向堆中弹出最值元素。
  3. 堆适合于数据量巨大的情况下的最大值或最大的前M项问题，它可以用可接受的空间流式地处理完所有数据。但它不擅长删除某个特定元素，因此我们可能需要一些辅助的数据结构来帮助堆标记已经删除掉的节点。
  4. 在Python中，结合列表和heapq库可以很方便地使用堆。

参考资料

  1. 《算法（第4版）》
  2. B站视频：【从堆的定义到优先队列、堆排序】 10分钟看懂必考的数据结构——堆
  3. Python文档：heapq --- 堆队列算法